Lista de MOOCs
Seleccione el curso de su preferencia, se puede inscribir con cualquier tipo de correo
 | Conjuntos y Álgebra
|
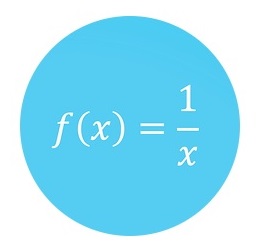 | Principios de Funciones I
|
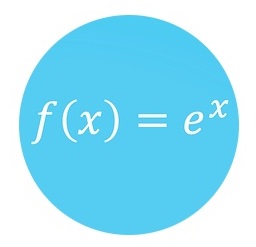 | Principios de Funciones II
|
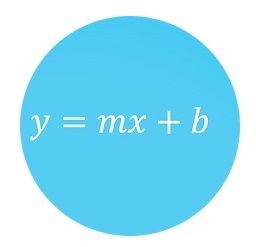 | Principios de Funciones III
|
 | Trigonometría
|
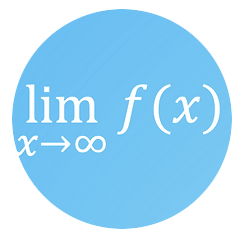 | Límites
|
 | Derivadas
|
 | Aplicaciones de la derivada
|
 | Integrales
|
 | Álgebra Lineal
|
¿QUIÉNES SOMOS?
Los cursos es 100% en línea, cada tema incluye videos, actividades interactivas, evaluaciones automatizadas y una sección de ejercicios.
Recomendamos en cada tema: (1) analizar cada uno de los videos; (2) realizar las actividades interactivas ; (3) efectuar las evaluaciones automatizadas, siempre se mostrará una solución detallada para que la persona participante la pueda contrastar; y, (4) hacer los ejercicios propuestos al final de manera individual y contrastar la solución que proporciona el curso.
Los cursos fueron creados por un equipo de profesores de la Escuela de Matemática de la Universidad de Costa Rica.
Contacto:
Profesor William Poveda Fernández, Dr.
william.poveda@ucr.ac.cr
